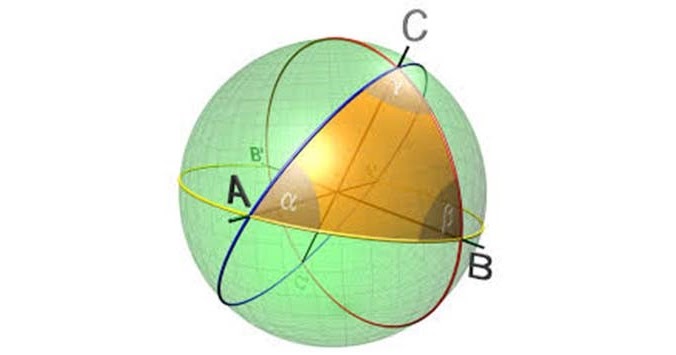
KÜRESEL GEOMETRİ
Şimdiye kadar bildiğimiz matematik bilgilerinin bir kısmının aslında tam olarak öyle olmadığını açıklayan küresel geometri, üçgenin iç açılarının toplamının 180 derece olmadığını ve aynı zamanda üçgenin alanı büyüdükçe iç açılarının da büyüdüğünü gösteren bir sistemdir. Aynı zamanda küresel geometriye göre bir noktanın dışındaki bir doğruya paralel doğru çizilemiyor ve doğrular iki noktada kesişen büyük çemberler olarak nitelendiriyor.
Şimdiye kadar mantığımıza yerleştirdiğimiz Öklid geometrisi düzlem yapılar için yeterlidir fakat küresel geometri üç boyutlu küresel cisimler için kullanılan gerçeğe daha yakın bir sistemdir.
Mesela üçgenin iç açılarının toplamının küresel geometriye göre aslında 180 derece olmadığını söyledik. Bu konuda aydınlanmak adına küresel bir şekilde herhangi üç noktayı ele alarak kavramaya çalışabiliriz. Bu üç noktanın birleşiminden bir üçgen oluşturduğumuzda bu üçgenin iç açıları 180 derece olmayacak. Örneğin bu ele aldığımız üç noktanın Ankara, İzmir ve İstanbul olduğunu varsayalım. Dünya düz değil yuvarlak yani küresel bir şekil olduğu için bu ele aldığımız noktaları birleştirip bir üçgen oluşturduğumuzda oluşan üçgenin iç açıları toplamının 180 dereceden fazla olduğunu görmüş oluruz.
Sonuç olarak astronomi alanında da büyük bir önem taşıyan küresel geometri bize gerçeğe en yakını sunan bir sistemdir. Böylelikle küresel şekiller üzerinden incelediğimiz şeyleri gerçeğe en yakın şekilde kavrarız.
KAYNAKÇA:
1- http://www.kozmikanafor.com/kuresel-geometri/
2- http://www.matematiksel.org/tag/kuresel-geometri/
HAZIRLAYAN: Fadime Nur DEMİRCİ